Handwriting Recogniser deep dive
This deep dive outlines the main concepts of the Handwriting Recogniser inner workings.
Neural networks
A neural network is an artificial representation of the human brain. It comprises computational nodes and their weighted interconnections, analogous to neurons and synapses. Input data flows though layers of nodes, with node output determined by incoming weights plus a mathematical function called an activation function.
Prior to user input, weights are randomly initialized and iteratively trained on training data, to refine the model, until one of the following occurs:
-
The training algorithm converges, meaning it reaches a stable value.
-
The specified number of iterations is reached.
Multilayer perceptron
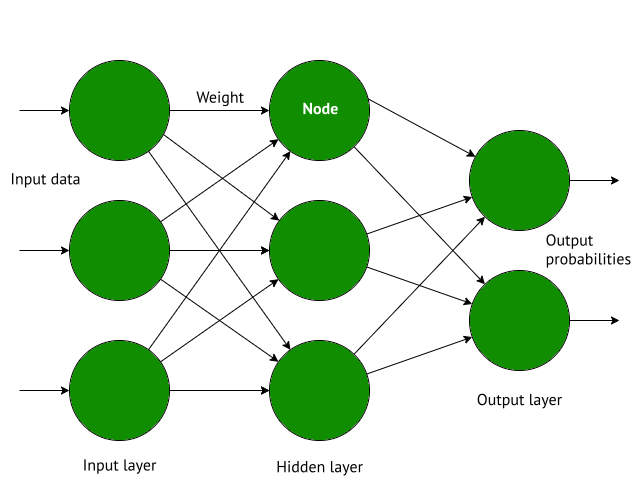
Handwriting Recogniser implements a multilayer perceptron (MLP) neural network trained on the MNIST database of handwritten numbers. An MLP consists of multiple layers, as illustrated in Figure 1:
-
Input layer: contains the input data
-
Hidden layer: calculates output to the next layer
-
Output layer: calculates the result
The hidden layer is the core of the network. It contains the functions that activate nodes and recalculate weights. The network can have multiple hidden layers, depending on the complexity of its functionality.
The MLP has the following characteristics, which are explained in following sections:
Feedforward processing
In a feedforward neural network, information flows in one direction, from input towards output. This design suits classification tasks, such as image recognition, because it allows an independent variable (the input to classify) to map to specified dependent variables (output classification options).
The alternative to feedforward is recurrent neural networks, whereby information can flow in loops. This allows memory within the network, making these networks suited for processing sequential data that relies on prior input, such as speech recognition data.
Backpropagation
The neural network uses its state, in terms of weights, to predict an outcome. During training, the discrepancy between predicted and actual outcome is calculated by a loss function, which is a mathematical representation of error, and this error must be minimised in order to optimise the network. Backpropagation is the calculation of the rate of change, or derivative, of the loss function, for each weight. Since a derivative indicates the direction in which a function increases, the negative of the derivative is used to indicate the direction of loss function minimisation and therefore optimisation.
Backpropagation only ascertains how to optimise the network, it does not perform the optimisation itself. Gradient descent performs the optimisation.
Gradient descent
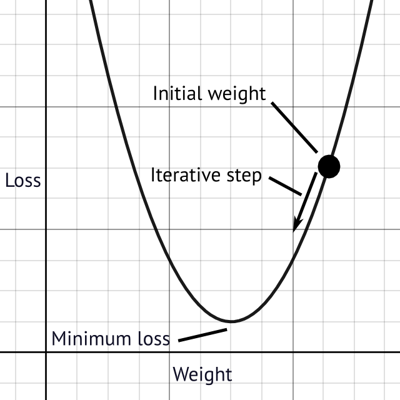
Gradient descent is an algorithm that descends the gradient defined by backpropagation. It amends the network weights iteratively until the loss function is minimised. This is analogous to descending a mountain peak, in steps, in the direction of the steepest slope, until the lowest valley is reached. See Figure 2 for a visualisation of the process.
Rectified Linear Unit activation function
An activation function calculates node output based on the input. If the output exceeds a defined threshold, the node is activated and passes data onwards through its outward connections. Activation functions are typically non-linear in order to introduce variance and therefore learn; a linear function would simply propagate input. Handwriting Recogniser uses the Rectified Linear Unit (ReLU) activation function, which returns output as equal to the input when the value is positive, otherwise it returns zero (see Figure 3).
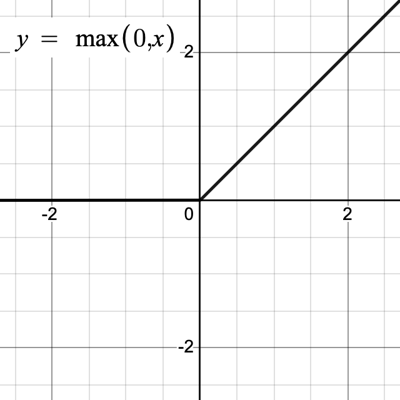
The activation function is also involved in the backpropagation derivative calculations. Notice that the derivative of ReLU is 0 for negative values and 1 for positive values, as illustrated in Figure 4.
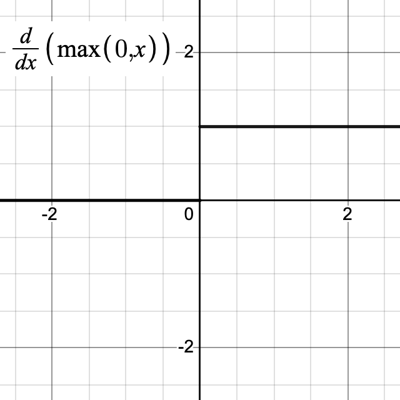
The derivative of the activation function is important for preventing the vanishing gradient problem, whereby the backpropagation derivatives prematurely approach 0 during gradient descent, causing the network to learn slowly or not at all. Vanishing gradients occur when implementing an activation function with derivatives that are close to 0 for many input values, such as the sigmoid function (see Figure 5).
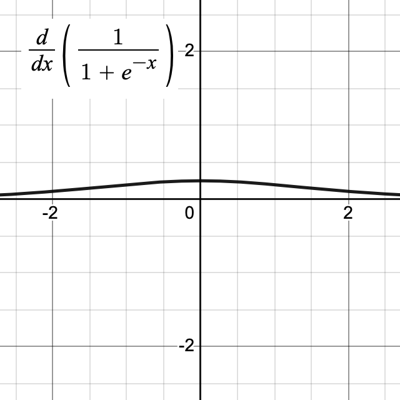
Softmax activation function
The softmax function is used in the final layer of the network, instead of the ReLU activation function, to output the result. It normalises the output values to probabilities of correctness between 0 and 1. These probabilities sum up to 1 and can therefore be regarded as percentages.
Learn more
-
See the Handwriting Recogniser tutorial for a practical guide of operations.
-
See the API specification for the full specification.